Bayesian Uncertainty Quantification via Machine Learning
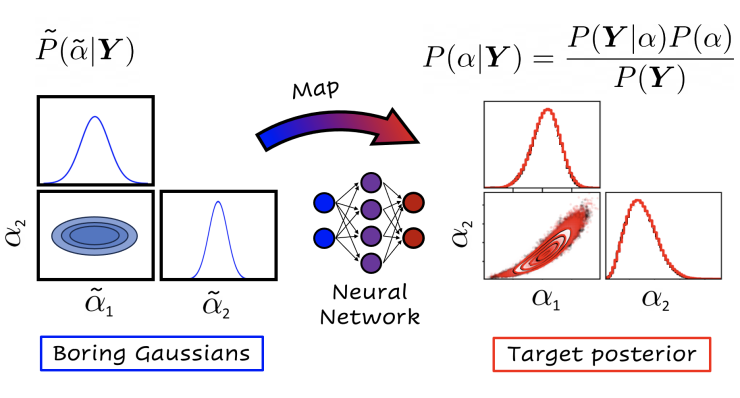
Image Credit: Pablo Giuliani/MSU
Student:
Lindsey Schneider
Mentor:
Yukari Yamauchi (Inspirehep), email: yyama122@uw.edu
Prerequisites:
None
What Students Will Do:
Students will learn about machine learning techniques, handling large data sets, and statistics. Students will program and test algorithms for the UQ study using normalizing flows and other computational tools as they come up. For the codes developed for [2], see https://gitlab.com/yyamauchi/rbm_nf. The codes developed by the students in this project will also be publicly available online. Students are also highly encouraged to learn about the theoretical models that will be used in this project.
Expected Project Length:
One year
Project Description:
One of the most important tasks in physics research is to build a solid connection between experiment and theory. From a theoretical point of view, one such connection is that the unknown parameters in theoretical models can be calibrated using relevant experimental data. For example, mass and charge radii of nuclei measured in experiments can constrain the model parameters of a theoretical model of mesons and nucleons [1]. When performing this calibration, it is crucial that we incorporate the errors from both experiment and theory—we call this process uncertainty quantification (UQ). In the past decade, Bayesian analysis has been used as a framework for UQ in nuclear physics and shown its wide applicability. One challenge in this framework is its computational cost: one needs to perform sampling from a high-dimensional posterior distribution, which is a distribution of the model parameters predicted by Bayesian analysis. Moreover, the calibration of the model parameters needs to be done continuously whenever new experimental data comes in and we update the calibration. Therefore, establishing an efficient sampling algorithm for such Bayesian analysis is an essential task for us to fully exploit the capacity that experiments possess in informing theoretical models. In [2], we showed that normalizing flows (a tool leveraging from the flexibility of machine learning) can speedup the sampling from the posterior distribution dramatically.
Following [2], the goal of the present project is to establish a concrete, efficient algorithm for continuously calibrating theoretical models with respect to experimental data with the help of normalizing flows and other tools from statistics and machine learning. The demonstration of the algorithm will be done with the relativistic mean field model used in [2] and other models as they come up. The project will be done in collaboration with the other authors at the Facility for Rare Isotope Beams.
References:
[1] P. Giuliani, K. Godbey, E. Bonilla, F. Viens, and J. Piekarewicz, Bayes goes fast: Uncertainty Quantification for a Covariant Energy Density Functional emulated by the Reduced Basis Method (2022), arXiv:2209.13039 [nucl-th].
[2] Y. Yamauchi, L. Buskirk, P. Giuliani, and K. Godbey, Normalizing Flows for Bayesian Posteriors: Reproducibility and Deployment (2023), arXiv:2310.04635 [nucl-th].
