Fuzzy Schwinger Model for Quantum Computation
Mentor:
Michael J. Cervia (INSPIRE-HEP, email: cervia@uw.edu)
Prerequisites:
Students will need to have previously studied intermediate-level electromagnetism (including the concept of gauge fixing) as well as classical and quantum statistical mechanics. Some basic programming experience will be helpful but not required.
What Students Will Learn:
Students will learn about lattice gauge theory, how computational techniques like tensor networks and quantum computation can come into play with nuclear and particle physics, and how to write classical and quantum programs in Python or C++ to evolve many-body systems.
Expected Project Length:
One year
Project Description:
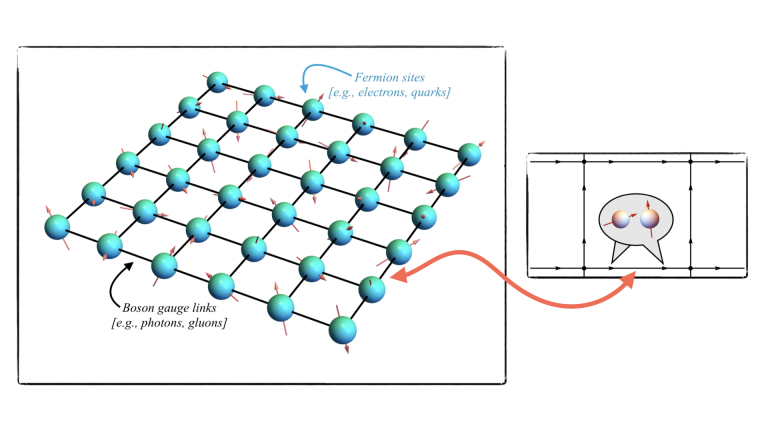
The strong nuclear force between quarks is mediated by gluons, massless color-charged particles with a spin quantum number 1. Gluons are bosons and so the number of them exchanged between even just two points in space can range from 0 to infinity. Classical computers work around this infinity by truncating allowed numbers at a large value, but are unable to calculate how this strong interaction evolves over time. Quantum hardware offers a way to see real-time evolution, but is much more limited for space, and so another workaround for this infinity would be required.
One proposal to efficiently encode states of gluons on quantum computers is the ‘fuzzy’ model of gauge theory [1]. The theory of quantum electromagnetism in one spatial dimension (sometimes called the Schwinger model) offers a simple and well-understood test case for using fuzzy gauge theory. We will perform a combination of classical [2] and quantum [3] computations to characterize this fuzzy Schwinger model and thereby assess how fuzzy models could facilitate quantum computations of gauge theory.
References:
[1] Andrei Alexandru, Paulo F. Bedaque, Andrea Carosso, Michael J. Cervia, Edison M. Murairi, and Andy Sheng. Fuzzy gauge theory for quantum computers. Phys. Rev. D, 109(9):094502, 2024.
[2] M. C. Bañuls, K. Cichy, K. Jansen, and J. I. Cirac. The mass spectrum of the Schwinger model with Matrix Product States. JHEP, 11:158, 2013.
[3] Stefan Kühn, J. Ignacio Cirac, and Mari-Carmen Bañuls. Quantum simulation of the Schwinger model: A study of feasibility. Phys. Rev. A, 90:042305, 2014.