INT 21R-1c Highlights Report
Tensor Networks in Many Body and Quantum Field Theory
April 3 - 7, 2023
S. Catterall, G. Evenbly, Y. Meurice, A. Roggero
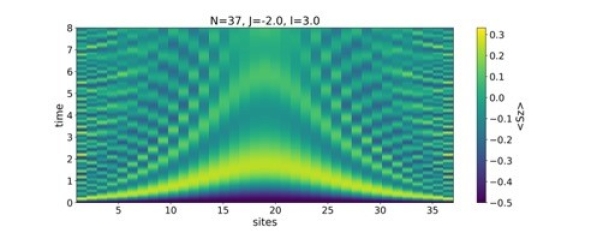
Time-evolution of a 1D hyperbolic chain using the Time
Evolving Blocked Decimation (TEBD) algorithm
(from participant Goksu Can Toga)
Tensor networks provide powerful numerical tools to study properties of strongly coupled models in condensed matter, nuclear and particle physics. They also constitute a jumping off place for the construction of lattice theories suitable for quantum computation and can serve as toy models for understanding holographic dualities. There has been rapid progress over the past decade on developing and extending the scope of such algorithms and tensor methods now constitute a significant component of a theorists arsenal for solving strongly interacting systems.
Following up to the online INT program with the same name that ran in June 2021, the INT hosted an in-person workshop during the week of April 3-7 2023. The goal of the program was to bring together theorists from condensed matter, particle and nuclear physics who are developing and using tensor networks to solve pressing physics problems - from understanding the ground states of entangled quantum matter to the formulation of networks for computing lattice path integrals and the elucidation of quantum information theoretic aspects of quantum matter together with the development of algorithms for quantum simulation.
The workshop provided a convenient arena for the interaction and exchange of ideas from communities that often have had little overlap in the past. Recent progress were reported on lifting path integral tensor methods to higher than two dimensions, improved coarse graining algorithms for fermions, qubit regularizations of spin and gauge models, applications to nuclear physics, and practical use of MPS and PEPS tensor networks for scalar, fermions and gauge fields.
Graphical illustrations of optimizations of fermionic tensor
networks (by participants Ryo Sakai and Patrick Emonts)
